Блог Makeomatic: разработка сайтов и мобильных приложений

Статистика

Прежде чем разбираться, как база данных оптимизирует запросы, давайте поговорим о статистике, потому что без неё любая база данных будет неэффективной. Если БД не анализирует собственные данные, её действия будут крайне неразумны. Какая же информация нужна БД для анализа?

Вкратце напомню, что для хранения данных операционные системы и БД используют минимальные единицы, называемые страницами или блоками — по умолчанию их размер составляет 4 или 8 килобайт. То есть если вам нужен всего 1 Кбайт, вы в любом случае займёте целый блок — в случае если его размер 8 Кбайт, из них 7 Кбайт вы потратите впустую.

Вернёмся к статистике.

Когда БД собирает статистику, она анализирует следующую информацию:

1. количество строк/страниц в таблице;
2. количество значений для каждого столбца в таблице;
3. длину соответствующих значений (мин, макс, среднее);
4. диапазон этих значений (мин, макс, среднее);
5. данные об индексах таблицы.

Эта информация помогает оптимизатору оценить потребление памяти и ресурсов ЦП и производительность дискового ввода/вывода для любого запроса.

Почему, например, необходимо собирать статистику для каждого столбца?

Предположим, в таблице PERSON мы собираемся объединить 2 столбца: фамилию (LAST_NAME) и имя (FIRST_NAME). Благодаря статистике, мы узнаем, что значений имён всего 1000, в то время как фамилий - 1 000 000. Поэтому база данных объединит значения в порядке LAST_NAME- FIRST_NAME (а не наоборот), таким образом она произведёт меньше операций сравнения - фамилии вряд ли будут совпадать, так что в большинстве случаев сравнения 2 или 3 первых букв будет достаточно.

Это простые примеры. Можно собирать расширенную статистику и графически представлять её в виде гистограммы, отражающей распределение значений в столбцах. Например, наиболее часто встречающиеся значения, квантили, и так далее.

Расширенная статистика помогает базе данных максимально оптимизировать запрос - особенно для вычисления предиката равенства (WHERE AGE = 18 ) или предиката диапазона (WHERE AGE > 10 and AGE <40 ) - проанализировав данные, БД будет знать количество строк, содержащих необходимую информацию (этот процесс называется «селективность»).

Хранится статистика в метаданных БД. Например, в однораздельных таблицах Oracle вы найдёте её в USER/ALL/DBA_TABLES и USER/ALL/DBA_TAB_COLUMNS, а DB2 хранит статистику в SYSCAT.TABLES и SYSCAT.COLUMNS.

Принципиально важно поддерживать статистические данные актуальными. Нельзя допускать, чтобы БД руководствовалась устаревшей информацией, например, что в таблице 500 строк, когда на самом деле там уже 1 000 000. Единственный минус статистики – на её вычисление требуется время. Поэтому в большинстве баз данных по умолчанию она не собирается автоматически. Естественно, когда у вас очень большие объёмы данных, процесс сбора статистики крайне затратен. В таких случаях лучше собирать только базовую статистику или анализировать небольшую выборку данных.

Например, когда я работал над проектом, где в каждой таблице были сотни миллионов строк, я анализировал только 10%, что сильно ускоряло процесс. К слову, в том случае это оказалось неудачным решением, потому что иногда те 10% данных для конкретного столбца конкретной таблицы, которые отбирает для анализа Oracle 10G, существенно отличаются от общих 100% данных. Неверная статистика привела к тому, что порой запрос занимал 8 часов вместо 30 секунд. Обнаружить причину такого поведения было нелегко.

Всё это лишний раз доказывает, какую важную роль играет статистика.
Конечно, в каждой базе данных есть свои специфические опции статистики. Чтобы узнать о них, внимательно ознакомьтесь с документацией к вашей БД. Я прочитал немало доков и, на мой взгляд, лучшая документации - у PostgreSQL.

Оптимизатор запросов

Все современные БД используют оптимизацию с учётом затрат (Cost Based Optimization). Идея в том, чтобы оценить каждую операцию по затратам ресурсов и времени выполнения и найти оптимальный способ выполнения запроса, используя минимальное количество операций и вычислительных ресурсов для получения результата.

Чтобы понять, как оптимизатор запросов работает и насколько это сложный процесс, нужны конкретные примеры. Мы рассмотрим 3 самых распространенных способа объединения двух таблиц, и вы поймёте, что даже простой запрос на объединение иногда сложно оптимизировать. А затем поговорим подробнее, как с этим справляются оптимизаторы баз дланных.

Для простоты мои примеры учитывают только временную сложность, а в базе данных оптимизатор учитывает затраты ресурсов процессора, памяти и операций ввода/вывода. Разница между временной сложностью и затратами процессора в том, что временные затраты – приблизительная величина (для лентяев вроде меня). Для вычисления процессорных затрат мне бы пришлось учитывать все операции — сложение, умножение, итерации, операторы if и так далее. К тому же, каждая высокоуровневая операция процессора состоит из нескольких низкоуровневых операций, и у разных процессоров (будь то Intel Core i7 или Intel Pentium 4 или AMD Opteron) они занимают разное количество ресурсов, в зависимости от архитектуры ЦП.

В общем, проще взять примеры на основе временной сложности — они тоже отлично проиллюстрируют идею оптимизации с учётом затрат. Поговорим немного и о затратах на операции ввода/вывода, это действительно важно - даже важнее процессорных затрат.

Индексы

Мы говорили об индексах в разделе про B+-деревья. Просто запомните, что эти индексы уже отсортированы. Ещё есть bitmap-индексы, но с точки зрения затрат ресурсов ЦП и памяти они считаются менее эффективными. Также в целях оптимизации многие современные базы данных могут динамически создавать временные индексы только для текущего запроса.

Пути доступа

До выполнения каких-либо операций с данными, их необходимо получить. Сделать это можно следующими способами.

Полное сканирование

Если вы когда-нибудь читали план выполнения запросов, то наверняка видели словосочетание “полное сканирование” (или просто сканирование), когда база данных считывает всю таблицу или индекс. Естественно, полное сканирование таблицы – более затраная операция, чем полное сканирование индекса.

Сканирование диапазона

Например, имея индекс в поле AGE, можно использовать сканирование индексного диапазона - “WHERE AGE > 20 AND AGE <40”.

Как вы помните, в части про B+-деревья мы выяснили, что запрос диапазона занимает log(N)+M времени, где N — количество данных в текущем индексе, а M — предполагаемое количество строк в этом диапазоне (M определяет селективность заданного предиката). Оба значения нам известны благодаря статистике. Сканирование диапазона не считывает весь индекс, что положительно сказывается на стоимости запроса.

Сканирование уникального значения

Наиболее выгодное решение, если вам нужно одно конкретное значение в индексе.

Доступ по id строки

Обычно при использовании индексов, базе данных приходится искать строки, связанные с этими индексами. Поиск этот осуществляется с помощью id строк.

Например, такой запрос:

1

SELECT LASTNAME, FIRSTNAME from PERSON WHERE AGE = 28

Если в столбце AGE есть индекс для PERSON, оптимизатор найдёт по индексу всех людей, возраст которых 28 лет, и запросит данные соответствующих строк в таблице, поскольку индекс обладает только информацией про возраст, а нам нужны также имя и фамилия.

Если мы изменим запрос:

1
2

SELECT TYPE_PERSON.CATEGORY from PERSON ,TYPE_PERSON
WHERE PERSON.AGE = TYPE_PERSON.AGE

Для объединения с TYPE_PERSON база данных использует индекс PERSON, но id строк в таблице PERSON запрашиваться не будет, поскольку нам не требуется информация из этой таблицы.

К сожалению, поиск id строк довольно затратная операция, поэтому если предполагается много подобных операций, лучше выбрать полное сканирование.

Помимо озвученных путей доступа в разных базах данных существуют и другие. Можете почитать подробнее в документации Oracle, терминология в разных БД может отличаться, но подходы те же.

Операторы объединения

Теперь, зная, как получить данные из БД, давайте объединим их! Рассмотрим три наиболее часто используемых операции объединения: объединение слиянием, хеш-объединение и объединение с помощью вложенных циклов. Но сначала разберёмся с двумя типами логических отношений — внутренним и внешним. Таблицы, индексы или промежуточные результаты от ранее выполненных операций (например результаты предыдущих объединений) могут быть взаимосвязанными. Когда мы объединяем два онтошения, алгоритмы объединения, в зависимотси от типа отношения, ведут себя по-разному. Далее я буду предполагать, что: “внешнее” отношение это находящийся слева набор данных, “внутреннее” отношение - правый набор данных.

Например, A JOIN B это объединение A и B, где A — внешнее отношение, B - внутреннее. Как правило, операции A JOIN B и B JOIN A отличаются по ресурсозатратности. Далее будем считать, что внешнее отношение содержит N элементов, а внутреннее - М элементов. Мы помним, что благодаря статистике оптимизатору БД известны N и M значения; эти значения определяют мощность множеств отношений.

Начнём с наиболее простого

Объединение с помощью вложенных циклов

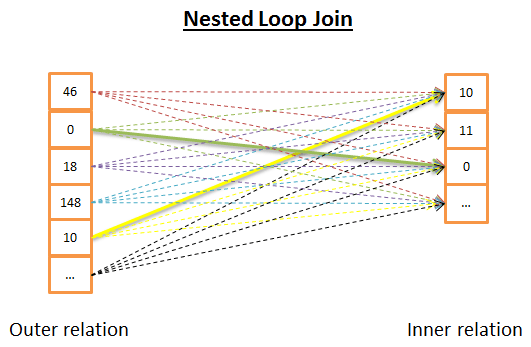
Суть объединения заключается в том, что для каждой строки внешнего отношения ищутся совпадения по всем строкам внутреннего отношения.

Происходит это примерно так:

1
2
3
4
5
6
7
8

nested_loop_join(array outer, array inner)
for each row a in outer
for each row b in inner
if (match_join_condition(a,b))
write_result_in_output(a,b)
end if
end for
end for

Из-за двойной итерации временная сложность составляет O(NM). С точки зрения операций ввода/вывода, для каждой из N строк внешнего отношения внутренний цикл должен считать M строк внутреннего отношения. То есть этот алгоритм считывает с диска Н + НМ строк. Если внутреннее отношение невелико, можно поместить его в память и считать лишь М + Н строк. Поэтому, чтобы поместиться в памяти, именно внутреннее отношение должно быть наименьшим.

В плане временной сложности нет никакой разницы, но для сокращения операций ввода/вывода оптимальнее считывать отношения только один раз. Также внутреннее отношение можно заменить на индекс, что лучше скажется на производительности.
Другой вариант данного объединения в случае, если внутреннее отношение не помещается в памяти, может быть таким: вместо считывания отношений построчно, вы считываете их группами строк, сохраняете в памяти 2 группы (по одной для каждого отношения), далее сравниваете строки в этих группах и сохраняете совпадения, затем загружаете новые группы и также сравниваете их, и так далее до конца.
Псевдокод этого объединения выглядит так:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

// улучшенная версия алгоритма для оптимизации затрат
nested_loop_join_v2(file outer, file inner)
for each bunch ba in outer
// ba сохранён в памяти
for each bunch bb in inner
// bb сохранён в памяти
for each row a in ba
for each row b in bb
if (match_join_condition(a,b))
write_result_in_output(a,b)
end if
end for
end for
end for
end for

В таком варианте временная сложность не изменяется, зато уменьшается количество обращений к диску. В первом варианте рассматриваемого алгоритма количество обращений составляло Н + НМ раз (по одному обращению на каждую строку). В улучшенной версии число обращений к диску составит количествогрупп(внешнего отношения) + количествогрупп(внешнего отношения) количествогрупп(внутреннего отношения). Увеличение размера групп строк позволит ещё больше сократить количество обращений к диску.

Стоит отметить, что с каждым обращением к диску считывается всё больший объём данных, но это не так важно, поскольку обращения последовательные (и наиболее критичным является время, необходимое для считывания первого набора данных).

Хеш-объединение

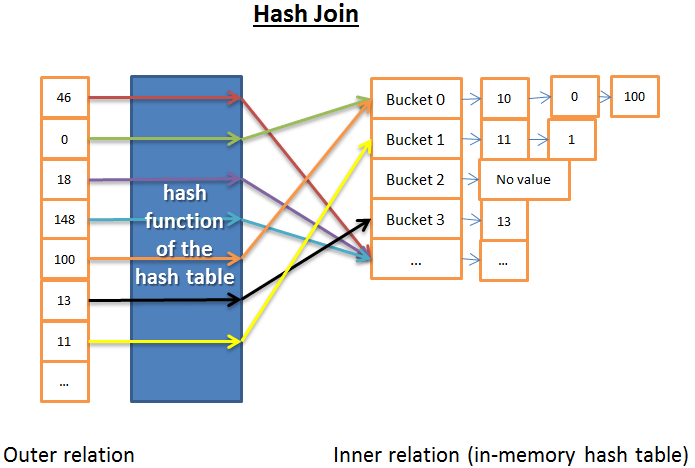
Хеш-объединение состоит из следующих шагов:

1. считать все элементы внутреннего отношения;
2. создать в памяти хеш-таблицу;
3. последовательно считать все элементы внешнего отношения;
4. с помощью функции хеш-таблицы вычислить хеш для каждого элемента и найти соответствующий ему сегмент внутреннего отношения;
5. найти совпадения между элементами данного сегмента и элементом внешнего отношения.

Для упрощения вычисления временной сложности этого алгоритма, будем считать что:

• внутреннее отношение делится на Х сегментов;
• хеш-функция равномерно распределяет хеш-значения для обоих отношений (то есть все сегменты одного размера);
• стоимость вычисления совпадения между элементом внешнего отношения и всеми элементами в сегменте пропорциональна количеству элементов в сегменте.

Таким образом, временную сложность можно вычислить так: (M/X) N + стоимостьсозданияхеш-таблицы(M) + стоимость_хеш-функцииN.
Если хеш-функция будет создавать небольшие по размеру сегменты, временная сложность составит O(M+N).

Есть еще один вариант хеш-соединения, который меньше загружает память, но более затратен с точки зрения операций ввода/вывода. Он состоит из следующих шагов:

1. создать хеш-таблицы для внутреннего и для внешнего отношений;
2. поместить их на диск;
3. сравнить отношения сегмент за сегментом (один сегмент загружается в оперативную память, а второй считывается построчно).

Объединение слиянием

Объединение слиянием - единственное объединение, которое выдаёт отсортированный результат.

В нашем упрощенном примере не будет разделения на внутренние и внешние таблицы, но в реальных, более сложных, примерах, алгоритм будет вести себя иначе, например при обнаружении дубликатов.

Объединение слиянием состоит из двух шагов:

1. (опционально) сортировка входных данных: данные сортируются по ключу объединения;
2. непосредственно слияние: отсортированные данные объединяются.

Сортировка

Мы уже говорили о cортировке методом слияния, в данном случае это сортировка слиянием в хорошем алгоритме (не лучшем, но хорошем — в ситуациях, когда нам важно экономить память).

Иногда входные данные отсортированы заранее, например, если таблица изначально сортируется по индексу условия объединения, или объединение применяется к промежуточному результату, ранее отсортированному в процессе запроса.

Объединение слиянием

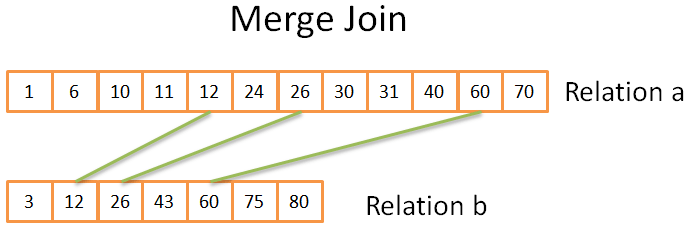
Этот этап очень похож на процесс слияния в рассмотренной нами ранее cортировке методом слияния. Но на этот раз выводится не каждый элемент из обоих отношений, а лишь совпадающие элементы.
Как это происходит:

1. сравниваем два текущих элемента двух отношений (текущий = первый, анализируемый впервые);
2. если они равны, то помещаются в результат вычисления, и процесс продолжается, перейдя на следующий элемент в каждом отношении;
3. если элементы не равны, алгоритм переходит в отношение с наименьшим элементом и берёт следующий элемент;
4. повторяем действия 1-2-3, пока не достигнем последнего элемента в одном из отношений.

Оба массива изначально отсортированы, поэтому не приходится “возвращаться” в них. Временная сложность составит O(M+N).
Если оба отношения изначально не отсортированы, тогда временная сложность пропорциональна затратам на сортировку обоих отношений: O(NLog(N) + MLog(M)).

Это упрощенная версия алгоритма, потому что у нас нет дубликатов, когда одни и те же данные несколько раз появляется в обоих массивах (соответственно, предполагая несколько совпадений). Если вы гуру алгоритмов и хотите взглянуть на более сложную версию, вот возможный алгоритм, обрабатывающий дубликаты:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

mergeJoin(relation a, relation b)
relation output
integer a_key:=0;
integer b_key:=0;
while (a[a_key]!=null and b[b_key]!=null)
if (a[a_key] < b[b_key]) a_key++; else if (a[a_key] > b[b_key])
b_key++;
else //предикат объединения выводит результат
write_result_in_output(a[a_key],b[b_key])
//Мы должны с осторожностью увеличивать указатели
integer a_key_temp:=a_key;
integer b_key_temp:=b_key;
if (a[a_key+1] != b[b_key])
b_key_temp:= b_key + 1;
end if
if (b[b_key+1] != a[a_key])
a_key_temp:= a_key + 1;
end if
if (b[b_key+1] == a[a_key] && b[b_key] == a[a_key+1])
a_key_temp:= a_key + 1;
b_key_temp:= b_key + 1;
end if
a_key:= a_key_temp;
b_key:= b_key_temp;
end if
end while

Какой алгоритм объединения лучше?

Если бы существовал «лучший» алгоритм объединения, не было бы всех остальных вариаций. Выбор зависит от множества факторов, например:

• объем свободной памяти: если у вас не достаточно памяти, можете даже не думать о хеш-объединении (по крайней мере его полном варианте с помещением хеш-таблицы в память);
• размер входных данных: например, если у вас одна таблица большая, а вторая очень маленькая, объединение вложенными циклами будет быстрее, чем хеш-объединение, в котором процесс вычисления хешей довольно затратен; в то же время если у вас обе таблицы очень большие, объединение вложенными циклами будет крайне затратным для ЦП;
• наличие индексов:работая с индексами двух В+-деревьев наиболее логичным выбором будет объединение слиянием;
• необходимость выполнить объединение в несколько процессов/потоков;
• необходимость сортировки результатов: даже работая с несортированными входными данными, вы, возможно, предпочтёте выбрать затратное объединение слиянием (с сортировкой), чтобы в итоге получить отсортированный результат, который можно соединить с результатами другого объединения слиянием (или просто потому что запрос через операции вроде ORDER BY/GROUP BY/DISTINCT предполагает отсортированные результаты);
• заранее отсортированные входные данные: в этом случае всё просто — выбирайте объединение слиянием;
• тип объединяемых отношений: это могут быть внешние или внутренние отношения, объединение по эквивалентности отношений (например, tableA.col1 = tableB.col2), декартово произведение и так далее. Некоторые алгоритмы объединений не работают с определёнными типами отношений;
• распределение данных: если данные для условия объединения несимметричны (например, вы объединяете людей по фамилии, но в таблице много однофамильцев), нельзя использовать хеш-объединение, потому что в таком случае хеш-функция создаст плохо распределённые сегменты.

Как обычно, для более глубокого ознакомления с темой отсылаю вас к документации DB2, ORACLE или SQL Server.

Упрощённый процесс выбора вида объединения

Итак, мы рассмотрели три вида операций объединения.

Теперь возьмём такой пример: предположим, нам необходимо объединить 5 таблиц, чтобы иметь полное представление о человеке. У человека (PERSON) может быть несколько мобильных номеров (MOBILES), почт (MAILS), адресов (ADDRESSES), банковских аккаунтов. (BANK_ACCOUNTS). И нам нужен быстрый результат на такой запрос:

1
2
3
4
5
6

SELECT * from PERSON, MOBILES, MAILS,ADRESSES, BANK_ACCOUNTS
WHERE
PERSON.PERSON_ID = MOBILES.PERSON_ID
AND PERSON.PERSON_ID = MAILS.PERSON_ID
AND PERSON.PERSON_ID = ADRESSES.PERSON_ID
AND PERSON.PERSON_ID = BANK_ACCOUNTS.PERSON_ID

Оптимизатор должен найти наиболее оптимальный способ обработки данных.
Перед ним встаёт два вопроса:

• Какой вид объединения их трёх (хеш-объединение, объединение слиянием, объединение вложенными циклами) использовать? И какие индексы - 0,1 или 2 (не говоря уже о том, что существуют различные типы индексов).
• В каком порядке выполнять цепочку объединений? Например, на рисунке ниже показаны разные возможные планы выполнения трёх объединений 4 таблиц:

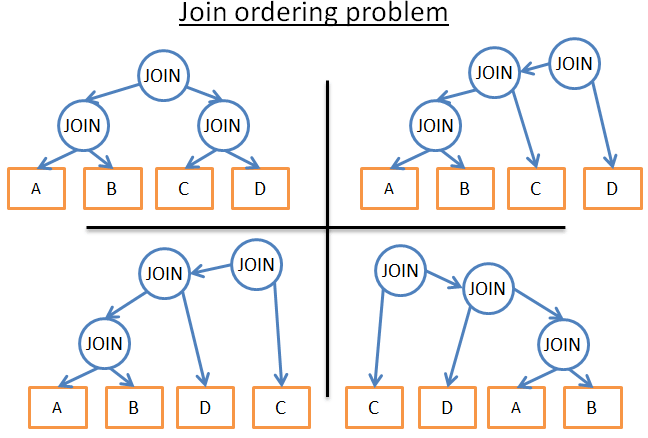
У оптимизатора есть следующие опции:

1. Брутфорс: Используя статистику базы данных, вычислить затраты для каждого возможного плана слияния и выбрать наилучший. Но здесть есть много вариантов. В заданной последовательности объединений каждое объединение может быть любым из трёх типов (хеш-объединение, объединение слиянием, объединение вложенными циклами). То есть для заданной последовательности объединений есть 34 возможных планов слияния. Выбор самой последовательности это по сути задача о перестановках и существует (24)!/(4+1)! возможных варианта. Таким образом, для решения этого простого примера оптимизатор должен выбрать из 34(2*4)!/(4+1)! или 27 216 возможных планов слияния. Если добавим в пример использование 0,1 или 2 индексов B+-деревьев, количество возможных планов слияния возрастёт до 210 000. И это, повторюсь, очень простой запрос.
2. Сразу сдаться и не выполнить запрос. Решение для слабаков;
3. Оценить лишь несколько планов слияния и выбрать наименее затратный. То есть вместо вычисления затрат на каждый возможный вариант, выбрать произвольное количество из всех возможных планов, оценить их стоимость и выбрать лучший из рассмотренных план слияния;
4. Применить «умные» условия, чтобы уменьшить количество возможных планов слияния. Есть 2 типа условий:
   a. Можно использовать «логические» условия, они исключат ненужные варианты, но не сильно уменьшат колитество возможных планов. Пример такого условия: «внутреннее отношение при объединении вложенными циклами должно быть наименьшим набором данных»
   b. Можно отказаться от поиска наилучшего решения и удовлетвориться просто хорошим, применив более жёсткие условия, чтобы существенно уменьшить количество возможных планов слияния. Например: «если отношение небольшого размера, использовать объединение вложенными циклами, и никогда не использовать объединение слиянием или хеш-объединение».

В одном простом примере у оптимизатора так много возможных вариантов. А в реальных запросах могут быть и другие операторы отношений: OUTER JOIN, CROSS JOIN, GROUP BY, ORDER BY, PROJECTION, UNION, INTERSECT, DISTINCT.

Как же база данных со всем этим справляется?

Динамическое программирование, жадный алгоритм и эвристика

Чтобы сделать правильный выбор, реляционная база данных пробует все вышеперечисленные подходы. Реальная задача оптимизатора заключается в том, чтобы найти эффективное решение за ограниченное количество времени. В большинстве случаев оптимизатор находит не «лучшее» решение, а «достаточно хорошее». Брутфорс-подход годится для небольших запросов. Но если использовать один полезный подход, избежав тем самым лишних вычислений, то можно применять брутфорс и для запросов средней величины. Этот полезный подход называется динамическое программирование.

Динамическое программирование

Основная идея, лежащая в основе динамического программирования, заключается в том, что многие планы выполнения запросов очень похожи.

Взгляните на рисунок ниже:

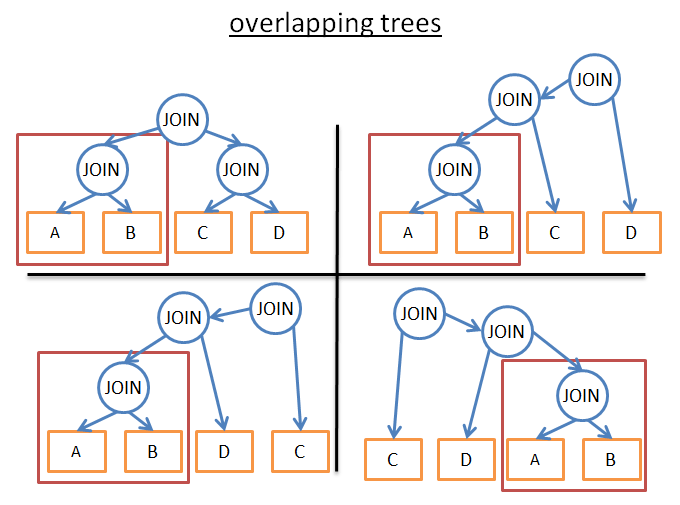
У всех представленных на рисунке планов есть общее поддерево A JOIN B. Поэтому, вместо вычисления стоимости затрат на выполнение этого поддерева в каждом плане, мы можем вычислить его один раз, сохранить полученное значение и использовать его каждый раз, когда встречается данное поддерево. Выражаясь формально, мы решаем проблему перекрытия. Чтобы избежать повторных вычислений, мы используем мемоизацию. Применив такой подход, вместо (2^N)!/(N+1)! временной сложности получаем сложность 3N. В нашем предыдущем примере с 4 объединениями, это бы означало уменьшить количество возможных планов выполнения с 336 до 81. Если взять запрос посложнее с 8 объединениями, такой подход уменьшит количество вариантов с 57 657 600 до 6561.

Для гуру алгоритмов, приведу пример, но объяснять его не буду — это пример для знатоков динамического программирования:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

procedure findbestplan(S)
if (bestplan[S].cost infinite)
   return bestplan[S]
// если bestplan[S] не был вычислен ранее, вычисляем сейчас
if (S contains only 1 relation)
         set bestplan[S].plan and bestplan[S].cost based on the best way
         of accessing S  /* Using selections on S and indices on S */
     else for each non-empty subset S1 of S such that S1 != S
   P1= findbestplan(S1)
   P2= findbestplan(S - S1)
   A = best algorithm for joining results of P1 and P2
   cost = P1.cost + P2.cost + cost of A
   if cost < bestplan[S].cost
       bestplan[S].cost = cost
      bestplan[S].plan = “execute P1.plan; execute P2.plan;
                 join results of P1 and P2 using A”
return bestplan[S]

Динамическое программирование можно использовать и для больших запросов, но с дополнительными условиями (эвристикой), для уменьшения количества вариантов, например:

• анализировать только конкрентый план, например, дерево с движением по левым ветвям, тем самым изменив временную сложность с 3^n на n*2^n

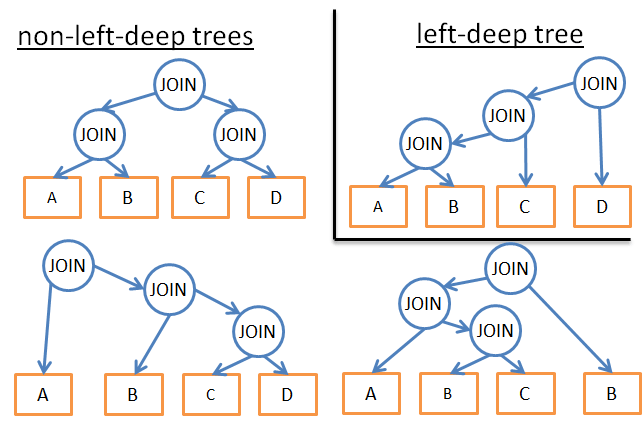
• добавить логические условия (например, «если таблица является индексом для данного предиката, применять объединение слиянием только к индексу, а не к таблице»); это сократит количество возможных вариантов, не исключая при этом наиболее эффективные решения.
• добавить правило для всего потока процессов (например, «выполнить операции объединения ДО всех остальных операций»), что тоже заметно сократит количество планов выполнения.

Жадные алгоритмы

Этот тип алгоритмов используют для очень больших запросов или когда нужно быстро получить ответ (на не очень быстрый запрос). Смысл такого алгоритма в том, чтобы выстраивать план выполнения запроса поэтапно, соблюдая определённые правила (эвристику). Алгоритм начинает план выполнения с одного объединения. Затем, на каждом последующем этапе, опираясь на то же заданное правило, алгоритм добавляет новое объединение к плану.

Рассмотрим несложный пример. Допустим, у нас есть запрос с 4 объединениями 5 таблиц (А, B, С, D, Е). Для упрощения задачи сразу выберем объединение вложенными циклами как единственное возможное объединение.

Давайте зададим правило «выполнять объединение с наименьшими затратами»:

• начинаем с одной из таблиц, например, с А;
• вычисляем стоимость каждого объединения с A (где A - либо внутреннее, либо внешнее отношение);
• устанавливаем, что A JOIN B — наименее затратное объединение;
• затем вычисляем стоимость каждого объединения с результатом A JOIN B (где A JOIN B - либо внутреннее, либо внешнее отношение);
• устанавливаем, что (A JOIN B) JOIN C - наименее затратное объединение;
• далее вычисляем стоимость каждого объединения с результатом (A JOIN B) JOIN C;
• и так далее…;
• в результате получаем план выполнения вида (((A JOIN B) JOIN C) JOIN D) JOIN E).

Поскольку мы произвольно начали с таблицы A, точно также можно применить этот алгоритм, начав с таблицы B, затем с C, с D и с E. И из полученных результатов выбрать план выполнения с наименьшими затратами.

Кстати, у данного алгоритма, который я назвал «жадным», есть и более благозвучное название - «алгоритм ближайшего соседа».

Не вдаваясь в дальнейшие подробности, применив сортировку Nlog(N), наш пример может быть решён. Стоимость данного алгоритма составляет O(Nlog(N)) или O(3N) в полностью «динамическом» его варианте. Таким образом, имея большой запрос из 20 объединений и применив этот алгоритм, мы получим всего 26 вариантов вместо 3 486 784 401 — огромная разница!

Проблема этого алгоритма в следующем: мы предполагаем, что найдя наилучшее объединение 2 таблиц, мы получим наиболее эффективный вариант, добавив к найденному объединению новое объединение. Однако, даже если A JOIN B даёт наиболее оптимальный по стоимости план объединения A, B и C, комбинация (A JOIN C) JOIN B может оказаться эффективнее, чем (A JOIN B) JOIN C. Поэтому для улучшения результата можно прогнать несколько жадных алгоритмов, установив разные правила, и по результатам выбрать самый оптимальный план.

Другие алгоритмы объединения

[Если алгоритмы уже сидят у вас в печёнках, переходите к следующему разделу: этот подраздел не так важен].
На самом деле, проблема поиска наилучшего плана выполнения — актуальная тема многих научных исследований. Обычно цель - найти наиболее эффективные решения для конкретных задач и внедрить их в БД. Например,

• в случае звездообразного объединения (это определенный тип запроса со множеством объединений), некоторые базы данных используют определенный, считающийся наилучшим, алгоритм.
• в случае параллельных запросов некоторые базы данных используют другой определенный алгоритм, и так далее.

Для замены динамического программирования в больших запросах, в данный момент изучаются разные алгоритмы. Жадные алгоритмы принадлежат к большой семье алгоритмов, называемых эвристическими алгоритмами. Как вы помните, жадный алгоритм следует определённому заданному правилу (эвристике), сохраняет результат, найденный на первом этапе, и переиспользует его для вычисления результатов последующих этапов. Некоторые алгоритмы соледуют заданному правилу, применяя его на каждом этапе, но не всегда запоминают наилучшее решение, найденное на предыдущем этапе. Они называются эвристическими алгоритмами.
Пример таких алгоритмов - генетические алгоритмы, в которых каждое найденное решение является возможным планом полного выполнения запроса, и вместо одного решения (т. е. плана), алгоритм находит P решений на каждом этапе вычислений:

1. сначала случайным образом создаётся Р количество планов;
2. сохраняются только планы с наименьшими затратами;
3. эти планы смешиваются и образуют новое P количество планов;
4. некоторые из новообразованных планов произвольно изменяются;
5. этапы 1-2-3 повторяются T количество раз;
6. и в конце сохраняется лучший план из P планов последнего цикла.

Таким образом, чем больше циклов проходит этот алгоритм, тем лучше результат.

Магия? Нет, законы природы: выживает только сильнейший!
Между прочим, генетические алгоритмы реализованы в PostgreSQL, но я не смог выяснить, используются ли они по умолчанию.

Существуют и другие эвристические алгоритмы, используемые в базах данных, например, симмулированная нормалиазция (Simulated Annealing), итеративное улучшение (Iterative Improvement), двухфазная оптимизация (Two-Phase Optimization). Но у меня нет информации, используют ли их уже в реальных БД, или пока только в экспериментлаьных базах данных.

Настоящие оптимизаторы

Но хватит теории. Мы программисты, а не исследователи, так давайте взглянем на реальные реализации.

Посмотрим, как работает SQLite оптимизатор.
Это облегчённая база данных, поэтому она использует простую оптимизацию на основе жадного алгоритма с определёнными правилами для сокращения количества вариантов:

• SQLite ни когда не меняет порядок таблиц в перекрестном объединении (CROSS JOIN);
• SQLite использует объединение вложенными циклами;
• внешние отношения вычисляются в порядке их следования;
• в версиях до 3.8.0 для поиска наиболее оптимального плана выполнения запроса SQLite использует «алгоритм ближайшего соседа»,
• начиная с версии 3.8.0, выпущенной в 2015 году, используется алгоритм «N ближайших соседей».

Давайте взглянем на другой оптимизатор от IBM – DB2 – он работает аналогично другим решениям в корпоративных базах данных, я выбрал его в качестве примера, поскольку до начала работы с большими данными использовал именно его.

Из официальной документации, мы узнаем, что DB2 оптимизатор позволяет применять 7 различных уровней оптимизации:

• возможность использования жадных алгоритмов для объединений:

1. с минимальной оптимизацией, используя сканирование индексов и объединение вложенными циклами, избегая переписывания части запросов,
2. с частичной оптимизацией;
3. с полной оптимизацией;

• возможность использования динамического программирования для объединений:

1. с умеренной оптимизацией и грубым приближением;
2. с полной оптимизацией, используя различные эвристические алгоритмы;
3. с полной оптимизацией, но без эвристики;
4. с максимальной оптимизацией без учёта ресурсозатрат и вычислением всех возможных последовательностей объединения, включая декартовы произведения.

Как видите, DB2 использует как эвристические алгоритмы, так и динамическое программирование. Конечно, вы не найдёте деталей реализации эвристики DB2, такие вещи держатся в секрете, ведь оптимизатор — важнейшая составляющая любой БД.

К слову, по умолчанию выбрана опция номер 5, когда оптимизатор использует следующие характеристики:

• использовать все возможные статистические данные, включая частотные распределения и квантили;
• применять все правила перезаписи запросов (в том числе таблицы маршрутизации материализованных запросов), за исключением ресурсозатратных правил, которые применяются в очень редких случаях;
• при динамическом переборе объединений ограниченно использовать составные внутренние отношения и декартовы произведения для звездообразных схем с таблицами подстановки;
• предоставлять большой выбор путей доступа, в том числе выборку предварительного списка (далее поговорим об этом подробнее), специальную операцию AND для индексов и таблицы маршрутизации материализованных запросов.

Остальные условия (GROUP BY, DISTINCT) обрабатываются простыми правилами.

Кэш плана запросов

Поскольку создание плана требует времени, большинство баз данных сохраняют план в кэше во избежание повторных вычислений одного и того же плана. Это в общем непростая задача, поскольку база данных должна знать, когда обновить устаревшие планы. Поэтому устанавливается некий предел, и когда количество изменений в статистических данных таблицы превышает этот предел, план запроса, связанный с этой таблицей, удаляется из кэша.

Диспетчер запросов

Наконец, мы вычислили оптимальный план выполнения запросов. Этот план компилируется в исполняемый код и, если ресурсов памяти и процессора достаточно, выполняется диспетчером запросов. Различные операторы (JOIN, SORT BY ) выпоняются последовательно или параллельно – это решает диспетчер. Для получения и записи данных диспетчер запросов взаимодействует с диспетчером данных, и именно о нём мы подробно поговорим в следующей части статьи.

По мотивам Christophe

To be continued…

Читайте так же статьи по теме:

• Как работает реляционная база данных. Часть 1
• Как работает реляционная база данных. Часть 3