Блог Makeomatic: разработка сайтов и мобильных приложений

Когда речь заходит о реляционных базах данных, становится очевидно, что информации по этой теме не хватает. Базы данных используются повсеместно, и они очень разные - от небольшой, но функциональной SQLite до мощной Teradata. И тем не менее, достойных, подробных статей, объясняющих как они работают, практически нет.

Можете погуглить “как работают реляционные базы данных”, и увидите, как мало результатов поиска. Да и те статьи, что есть, довольно короткие. Если же погуглить что-нибудь из последних трендов (большие данные, базы данных типа NoSQL или JavaScript), вы найдете в разы больше хороших источников информации.
Значит ли это, что реляционные базы данных устарели, и писать о них вне университетских курсов и научных статей уже не модно?

Я разработчик и ненавижу использовать то, чего не понимаю. Раз базы данных используются в разработке вот уже 40 лет, значит, на то есть весомая причина. За эти годы я потратил сотни часов, чтобы понять эти странные ящики пандоры, которые использую каждый день. На самом деле, реляционная база данных – интересная концепция, основанная на полезных, повторяющихся идеях. Если вы всегда хотели углубить ваши знания и понимание баз данных, но не хватало времени или желания разбираться в столь обширной теме, эта статья вам понравится.

Хотя название говорит само за себя, уточню: для понимания данной статьи вам необходимо знать, как написать простой запрос на соединение и базовый CRUD запрос. Только и всего. Всё остальное я объясню.

Начну с таких основ информатики, как временная сложность алгоритма. Наверное, многие из вас эту тему терпеть не могут, но без неё вы не сможете понять всю гениальность баз данных. Поскольку тема большая, я сосредоточусь на том, что считаю наиболее важным: как база данных обрабатывает SQL-запрос. Мы рассмотрим самые простые концепции, так что к концу статьи у вас должно сложиться полное представление о том, что такое БД.

Статья техническая и длинная, в ней много говорится про алгоритмы и структуры данных - не торопитесь дочитать до конца. Какие-то моменты сложнее понять, и пропуская их при первом прочтении, у вас всё равно должна сложиться полноценная картина.

Статья условно разделена на три части:

• Обзор низкоуровневых и высокоуровневых компонентов БД;
• Разбор процесса оптимизации запросов;
• Управление транзакциями и буферным пулом БД.

Начнём с азов

Давным-давно (в другой галактике…) разработчикам приходилось запоминать количество совершаемых операций. Они знали наизусть свои алгоритмы и структуры данных, поскольку не могли позволить себе тратить память и мощности своих довольно медленных компьютеров на подобные задачи.

В этой части, я буду напоминать вам о некоторых концепциях из тех далёких времён, поскольку они крайне важны для понимания баз данных. Также мы рассмотрим понятие индекс базы данных.

Временная сложность

O(1)) vs O(n^2)
Сегодня временная сложность алгоритмов не волнует почти никаких разработчиков. Но когда вы начинаете работать с большим объемом данных, или если вам приходится бороться за каждую лишнюю миллисекунду - при работе с базами данных вы рано или поздно столкнётесь и с тем, и с другим, - понимание данной концепции становится очень полезным. Не буду слишком долго утомлять вас разглагольствованиями, только о главном - это поможет нам впоследствии понять принцип оптимизации с учётом затрат.

Временная сложность определяет, сколько времени алгоритм будет обрабатывать конкретный объем данных. Для математического обозначения используется заглавная О и функция, вычисляющая, сколько операций необходимо алгоритму для заданного количества данных.

Проще говоря, формула вида O(некая_функция()) расшифровывается так: для определённого количества данных алгоритму требуется некая_функция(количество_данных) операций.

И важно здесь не количество входных данных, а то, как увеличивается количество необходимых операций с увеличением количества данных. Временная сложность не расчитывает точное число операций, но даёт довольно чёткое представление.

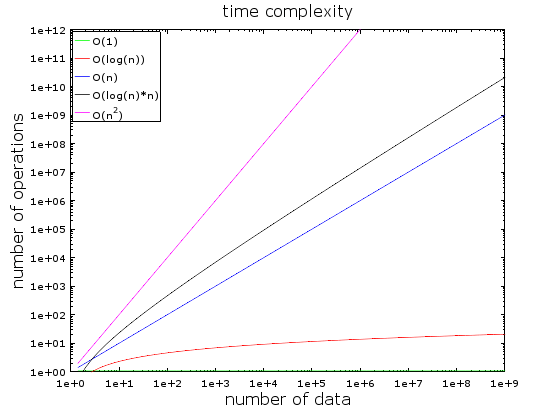
На этом графике вы видите разные временные сложности. Для его создания я использовал логарифмическую шкалу - количество данных резко возрастает от 1 до 1 миллиарда.

Мы видим, что:

• Значение О (1) остается неизменным (поэтому она называется постоянной сложностью);
• Значение О (log(n)) остаётся маленьким даже при больших объёмах данных;
• Хуже всего показатель сложности О (n^2), где количество необходимых операций быстро
  возрастает;
• Значения двух оставшихся кривых также быстро растут.

Разберём примеры подробнее:

При небольшом объёме данных разницы между О(1) и O(n^2) практически нет. Предположим, у вас есть алгоритм, который должен обработать 2000 элементов.

• Алгоритму O(1) потребуется всего 1 операция;
• Алгоритму O(log(n)) - 7 операций;
• Алгоритм O(n) обойдётся вам в 2 000 операций;
• Алгоритм O(n*log(n)) – уже в 14 000 операций;
• Наконец, алгоритму O(n^2) потребуется 4 000 000 операций.

Разница между O(1) и O(n^2) кажется огромной (4 миллиона), но на самом деле это всего около 2 миллисекунд — и моргнуть не успеете. Современные процессоры способны выполнять сотни миллионов операций в секунду. Поэтому для большинства IT-проектов производительность и оптимизация не являются критическими проблемами.
Однако, когда вы сталкиваетесь с огромным количеством данных, эти знания вам очень пригодятся. Допустим, теперь алгоритм должен обработать 1 000 000 элементов (не так уж много для базы данных):

• Алгоритму O(1), как и прежде, потребуется 1 операция;
• Алгоритму O(log(n)) - 14 операций;
• Алгоритм O(n) займёт 1 000 000 операций;
• Алгоритм O(n*log(n)) – 14 000 000 операций;
• Алгоритм O(n^2) - 1 000 000 000 000 операции.

Точно не считал, но навскидку за время выполнения O(n^2) вы успеете отойти выпить чашку кофе (возможно, две). Добавьте к изначальному количеству элементов ещё один ноль — и на время выполнения последнего алгоритма можно лечь поспать.

Если ближе к практике, можно привести такие примеры:

• Поиск элемента в правильной хеш-таблице занимает O(1) операций;
• Поиск в сбалансированном дереве выдаст результат за O(log(n)) операций;
• Поиск в массиве - пример O(n);
• Лучшие алгоритмы сортировки имеют O(n*log(n)) временную сложность;
• Плохие алгоритмы сортировки — сложность O(n^2).

Временная сложность бывает среднестатистической, а также наилучший и наихудший сценарии. Чаще всего, подразумевается худший сценарий.

Также при выполнении алгоритма учитывается потребление памяти и производительность при чтении и записи на диск.

Конечно, есть сложности и похлеще n^2:

• n^4: это кошмар! я буду упоминать некоторые алгоритмы с такой сложностью;
• 3^n: просто ад; мы встретим один такой алгоритм примерно в середине статьи (и, он, к слову, используется во многих БД);
• факториальный n: результатов вы не дождётесь никогда, даже при небольшом объёме данных;
• n^n: если вы используете алгоритмы такой сложности, возможно, стоит спросить себя, а стоит ли мне дальше работать в IT-сфере.

Я не дал точного определения “большого О”, только общую идею. Изучить подробнее можете в этой Wiki статье.

Сортировка методом слияния

Что вы делаете, когда нужно отсортировать коллекцию? Вызываете функцию sort()? Окей, но для работы с базами данных хорошо бы понимать, как эта функция работает.

Есть несколько хороших алгоритмов сортировки, я остановлюсь на наиболее важном: сортировка методом слияния. Возможно, сейчас вы не очень понимаете, чем так полезна сортировка данных, но когда мы поговорим об оптимизации запросов, вы поймёте. К тому же, понимание этого алгоритма поможет нам позднее понять типичную для БД операцию объединения, которую ещё называют объединение слиянием.

Слияние

Как и многие полезные алгоритмы, сортировка методом слияния основана на хитрости: слияние двух отсортированных массивов размера N/2 в отсортированный массив из N-элементов займёт всего N операций. Эта операция называется слиянием.

Посмотрим на простом примере, что это значит:

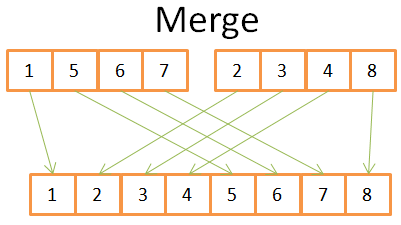
По рисунку видно, что для построения отсортированного массива из 8 элементов нам нужно перебрать два массива из 4х элементов всего 1 раз.
Поскольку оба массива из 4 элементов уже отсортированы, мы:

1. сравниваем два текущих элемента в 2 массивах (текущий = первый, анализируемый впервые);
2. наименьший из них помещаем в массив из 8 элементов;
3. и переходим к следующему элементу в массиве, откуда был взят наименьший элемент;
   повторяем действия 1-2-3, пока не дойдём до последнего элемента в одном из массивов. Затем уже берём оставшиеся элементы другого массива и помещаем их в наш конечный массив из 8 элементнов.

Оба массива из 4 элементнов изначально отсортированы, поэтому не приходится возвращаться в них.

Таким образом, сортировка методом слияния разбивает задачу на небольшие задачи, и находит результат этих более мелких задач, чтобы в итоге получить результат исходной задачи (такой вид алгоритмов можно назвать «разделяй и властвуй»). Если вдруг алгоритм всё равно вам не понятен, не расстраивайтесь, я не понял его с первого раза. Можете дополнительно ознакомиться со статьёй в википедии.

Я условно разделяю алгоритм на две стадии:

1. стадию деления, когда массив делится на более мелкие массивы;
2. стадию сортировки, когда небольшие массивы соединяются (слиянием), чтобы сформировать один общий массив.

Стадия деления

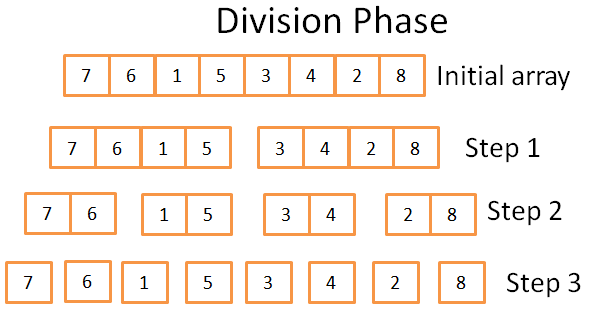
На стадии деления данный массив разбивается на унитарные массивы в 3 шага. Формальное число шагов можно обозначить как log(N) (т.к. N = 8, log(N) = 3).
Откуда мне это известно?
Я гений! Шучу, одним словом — математика. Идея заключается в том, что каждый шаг делит размер исходного массива на 2. Количество шагов отражает, сколько раз можно разделить исходный массив на два. Это определение логарифма (по основанию 2).

Стадия сортировки

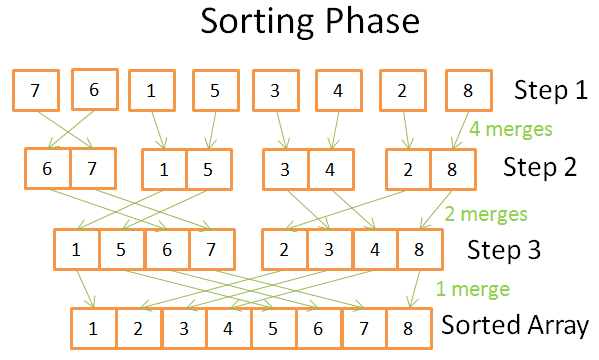
На стадии сортировки мы начинаем с унитарных массивов. На каждом шаге выполняем несколько слияний, и общее число операций составляет N = 8:

Первый этап: 4 слияния, каждое по 2 операции;
Второй этап: 2 слияния, 4 операции каждое;
На третьем этапе: 1 слияние в 8 операций.

Этапов всего log(N), то есть N * log(N) операций.

Преимущества сортировки методом слияния

Так почему же этот алгоритм такой особенный?

Во-первых, его можно изменить, уменьшив тем самым объем занимаемой памяти, так что вам не нужно создавать новые массивы, а лишь непосредственно изменять исходный массив.
Такие алгоритмы называются локальными.

Во-вторых, вы можете изменить его и использовать одновременно дисковое пространство и небольшой объем памяти, без затратных операций чтения и записи на диск. Идея в том, чтобы загружать в память только те части, которые в данный момент обрабатываются. Это очень актуально, когда вам нужно отсортировать многогигабайтную таблицу с буфером памяти лишь 100 Мб. Такие алгоритмы называются внешней сортировкой.

К тому же, можно сделать так, чтобы алгоритм работал на нескольких процессах / потоках / серверах. Например, распределенная сортировка слиянием - один из ключевых компонентов Hadoop (фреймворк для больших данных).
В общем, этот алгоритм может превратить свинец в золото (правда ведь!).

Данный алгоритм сортировки используется в большинстве баз данных (если не во всех), но он не единственный. Если хотите знать больше, можете прочитать эту научную работу, в которой рассматриваются плюсы и минусы основных алгоритмов сортировки в БД.

Массив, дерево и хеш-таблица

Теперь, когда вы знаете о временной сложности и сортировке, я должен рассказать вам о 3 структурах данных. Это важно, так как это основы современных баз данных. Также рассмотрим понятие индекс базы данных.

Массив

Двумерный массив является простой структурой данных. Таблица может рассматриваться как массив. Например:

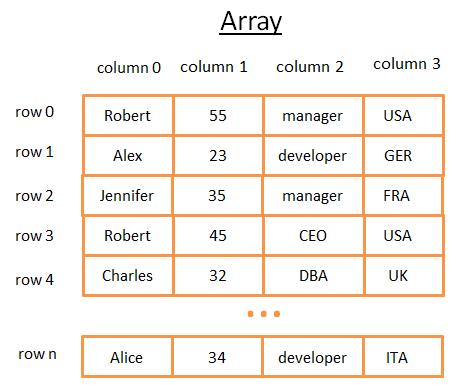
Этот двумерный массив представляет собой таблицу со строками и столбцами. Каждая строка представляет собой предмет. Столбцы — признаки, описывающие предметы. Каждый столбец хранит определенный тип данных (целое число, строка, дата …). Для хранения и визуализации данных это удобно, но когда вам нужно найти конкретное значение — это кошмар.

Например, если вам потребуется найти всех людей, работающих в Великобритании, вы должны анализировать каждую строку, чтобы узнать, из Великобритании ли этот человек. Это займёт у вас N операций (где N - число строк), что не плохо, но могло быть и быстрее? Тут-то в игру вступают деревья.

К слову, для более эффективного хранения таблиц большинство современных баз данных обеспечивают расширенные массивы, как таблицы куч или таблицы индексов. Но это не меняет проблемы быстрого поиска по конкретному условию в группе столбцов.

Дерево и индекс БД

Двоичное дерево поиска - это бинарное дерево с особыми свойствами, ключи в каждом узле должны быть больше всех ключей, хранящихся в левом поддереве, и меньше всех ключей, хранящихся в правом поддереве.

Наглядный пример:

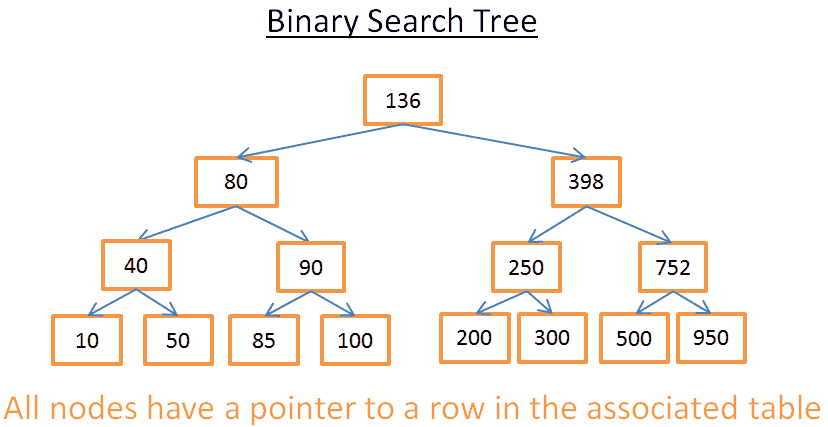
Это дерево состоит из N = 15 элементов. Допустим, я ищу 208:

• Начинаем с корня, у которого ключ 136. Поскольку 136 < 208, ищем в правом поддереве узла 136;
• 398 > 208, поэтому далее ищем в левом поддереве узла 398;
• 250 > 208, поэтому перемещаемся в левое поддерево узла 250;
• 200 < 208, соответственно, надо искать в правом поддереве узла 200. Но 200 не имеет правого поддерева, то есть значение не существует (если бы существовало, оно должно было бы находиться в правом поддереве 200).

Допустим, теперь я ищу 40:

• Начинаем с корня, у которого ключ 136. Поскольку 136 > 40, ищем в левом поддереве узла 136;
• 80 > 40, поэтому далее ищем в левом поддереве узла 80;
• 4 0 = 40, узел существует. Извлекаем id строки внутри узла (на картинке его нет) и ищем в таблице строку с данным id.

Зная id строки, я точно знаю, где именно в таблице находятся нужные данные и могу сразу же их получить.

В итоге, оба поиска заняли количество операций, равных количеству уровней внутри дерева. Если вы внимательно читали раздел о сортировке методом слияния, то увидите, что количество уровней - log(N). Таким образом, сложность поиска - log(N).

Назад к нашей проблеме

Но это всё довольно абстрактные вещи, давайте вернемся к нашей проблеме. Вместо глупого целого числа теперь страну в предыдущей таблице обозначает строка. Предположим, у вас есть дерево, которое содержит столбец таблицы “страна”:

Если задача - узнать, кто работает в Великобритании, вы ищете в дереве узел, представляющий Великобританию, внутри этого узла вы найдете расположение строк работников из Великобритании. Если вы напрямую используете массив, этот поиск потребует log(N) операций (вместо N операций). Это и есть индекс базы данных.

Вы можете построить дерево индекса для любой группы столбцов (строка, целое число, две строки, дата …) при условии, что у вас есть функция для сравнения ключей (т.е. группа столбцов), так что вы можете установить порядок среди ключей (что характерно для большинства БД).

Индекс B+-деревьев

Поиск определённого значения в таком дереве работает неплохо, но проблемы начинаются, когда нужно найти несколько элементов между двумя данными значениями. Это займёт O(N) времени, поскольку вам придется анализировать каждый узел в дереве и проверять, есть ли он между этими двумя значениями (например, обход дерева с порядковой выборкой). Кроме того, эта операция негавтино сказывается на производительности, поскольку вы обрабатываете всё дерево целиком. Неплохо бы найти более эффективный способ запроса диапазона. Для этого современные базы данных используют модифицированную версию дерева под название B+. В таком дереве только нижние узлы (листья) хранят информацию (расположение строк в соответствующей таблице), остальные узлы во время поиска приводят к нужному узлу.

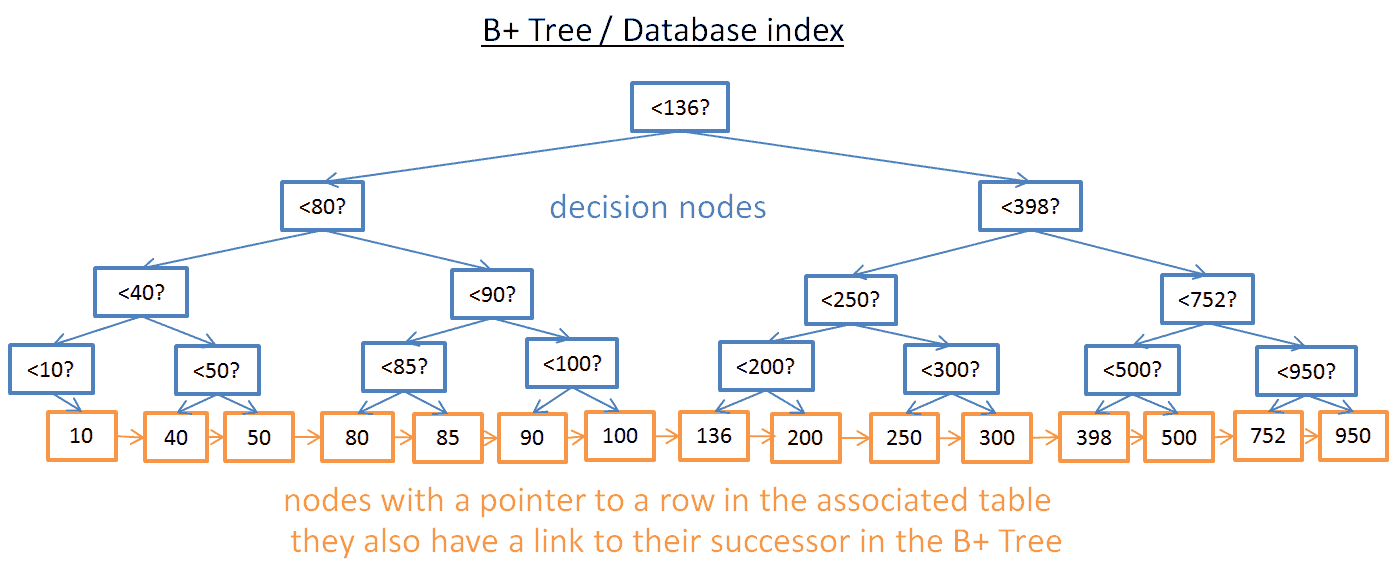
Как видите, узлов больше (в два раза). Действительно, это дополнительные, «решающие» узлы, которые помогут найти нужный узел (хранящий расположение строк в соответствующей таблице). Но сложность поиска все еще O(log(N)) (добавлен лишь ещё один уровень). Большая разница в том, что самые нижние узлы связаны с вышестоящими преемниками.

В таком B+-дереве, если вы ищете значения между 40 и 100:

• Вы просто должны искать 40 (или ближайшие значения после 40, если 40 не существует), как мы делали в предыдущем примере с деревом;
• Затем получить преемников 40, используя прямые ссылки на них, пока не достигнете 100.

Допустим, вы нашли М преемников и дерево имеет N узлов. Поиск конкретного узла займёт log(N) времени, как и в предыдущем дереве. Но, как только у вас есть этот узел, вы находите в M операций М преемников со ссылками на их преемников. Этот поиск стоит всего М+log(N) операций, а не N операций, как в примере с предыдущим деревом. Кроме того, вам не нужно читать полное дерево (только М + log(N) узлов), то есть меньше используется диск. Если значение M невелико (например, 200 строк), а N большое (1 000 000 строк), разница будет существенной.

Но теперь появились новые проблемы! Если добавить или удалить строку в базе данных и, следовательно, в соответствующем индексе B+-дерева:

• вы должны сохранить порядок следования узлов внутри дерева, в противном случае вы не сможете найти узлы внутри беспорядочной массы;
• вы должны стремиться к минимально возможному числу уровней в B+-дереве, иначе временная сложность O(log(N)) превратится в O(N).

Таким образом, В+-дерево должно быть самоупорядоченным и сбалансированным. К счастью, это возможно с помощью смарт-удаления и вставки операций. Но у всего есть своя цена: операции вставки и удаления в B+-деревьях имеют сложность O(log(N)). Поэтому вы, возможно, знаете, что использовать очень много индексов - плохая идея. Вы замедляете быстрые вставку/обновление/удаление строки в таблице, поскольку базе данных нужно обновить индексы таблицы, а это дорогостоящая O(log(N)) операция на каждый индекс. Кроме того, добавление индексов значит больше нагрузки для диспетчера транзакций (мы поговорим о нём в конце статьи).

Более подробную информацию о B+-деревьях можете прочитать в статье в Википедии. Если хотите пример B+-Tree реализации в базе данных, изучите эту статью или эту от главного разработчика MySQL. Обе статьи описывают, как InnoDB (движок MySQL) обрабатывает индексы.

Примечание: один читатель заметил, что из-за низкоуровневой оптимизации В+-дерево должно быть полностью сбалансированным.

Хэш-таблица

Последняя важная структура данных, которую мы рассмотрим, - хеш-таблицы. Они очень полезны, когда нужно быстро получить нужное значение. Понимание хеш-таблиц поможет нам в дальнейшем понять типичную для БД операцию хеш-соединения. Эта структура данных также используется базами данных для хранения внутренних составляющих (например, таблиц блокировок или буферного пула, мы рассмотрим оба понятия позже).

Хеш-таблица - это структура данных, которая быстро находит элемент с ключом. Для построения хеш-таблицы необходимо определить:

• ключ для элементов;
• хеш-функцию для ключей; вычисленные хеши ключей определяют расположение элементов (и называются сегментами (buckets));
• функцию для сравнения ключей; как только вы нашли нужный сегмент, необходимо найти нужный элемент внутри данного сегмента с помощью этой функции.

Простой пример

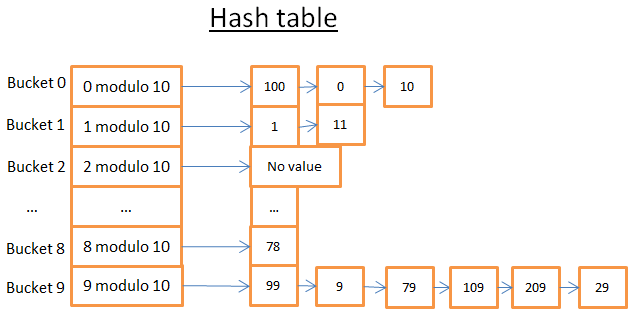
В данной хеш-таблице 10 сегментов. Из-за великой лени я нарисовал всего 5, но уверен, ваше воображение дорисует ещё 5. Я использовал хеш-функцию с ключом по модулю 10. Другими словами, я храню только последнюю цифру ключа элемента, чтобы найти его сегмент.

• если последняя цифра 0, элемент попадает в сегмент 0;
• если последняя цифра 1, элемент попадает в сегмент 1;
• если последняя цифра 2, элемент попадает в сегмент 2, и так далее.

В качестве функции для сравнения я использовал простое равенство двух целых чисел.
Допустим, нам нужен элемент 78:

• хеш-таблица вычисляет хеш код для 78, равный 8;
• первый элемент в сегменте 8 и есть нужный нам элемент 78.

Поиск занимает всего 2 операции – первая вычисляет хеш код, вторая находит элемент в конкретном сегменте.

Например, теперь мы ищем 59:

• хеш-таблица вычисляет хеш код – 9;
• первым элементом в сегменте 9 оказывается 99; поскольку 99 не равно 59, поиск продолжается;
• далее по той же логике анализируется второй элемент (9), и следующий за ним (79) и так далее до последнего элемента в сегменте (29);
• в данном случае необходимого элемента 59 не существует.

Поиск занимает 7 операций.

Правильная хеш-функция

Как видите, количество необходимых операций от поиска к поиску может меняться.
Если я заменю фунцию из предыдущего примера на функцию с ключом по модулю 1 000 000, поиск займёт всего 1 операцию, потому что в сегменте 000059 нет элементов. Главная цель – выбрать такую хеш-функцию, которая создаст сегменты с небольшим количеством элементов.

В моём примере найти подходящую хеш-функцию было не трудно – потому что пример простой. Когда ключом является строка (например, фамилия), 2 строки (фамилия и имя), 2 строки и дата (фамилия, имя и дата рождения), найти хорошую функцию уже гораздо сложнее.

Когда хеш-функция удачная, сложность поиска по хеш-таблице составляет O(1).

Массив или хеш-таблица

А почему бы не использовать только массивы?
Хеш-таблица может быть лишь наполовину загружена в память, остальная половина сегментов будет на диске, а для массива вы должны использовать непрерывное пространство памяти. Если вы работаете с большой таблицей, непрерывного пространства обычно не хватает. С хеш-таблицей вы можете выбрать любой ключ (например, страна и фамилия человека).

Можете также ознакомиться с моей статьёй, где разобран пример эффективной Java хеш-таблицы; вам совсем не обязательно знать Java, чтобы понять статью.

Компоненты БД

Мы посмотрели на основные компоненты БД. Взглянем на всю картину в целом.

База данных это набор информации, которую легко получать и изменять. Но то же самое можно сказать о куче файлов. На самом деле, простейшие базы данных вроде SQLite это и есть куча файлов. Но продуманная и организованная куча файлов, потому что только БД позволяет использовать транзакции, обеспечивающие верную последовательность и безопасность данных, а также обрабатывать данные быстро, даже когда вы имеете дело с миллионами данных.

Общая структура БД выглядит примерно так:

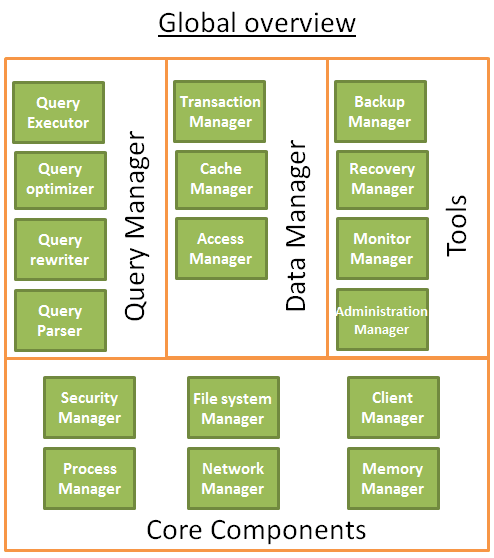
Перед написанием этой части я прочитал немало книг/статей, и каждый источник описывал БД по-своему. Так что не зацикливайтесь особо на том, как я организовал эту базу данных или как назвал процессы, я старался, чтобы данная часть гармонично вписывалась в общий план статьи. Главная идея в том, что БД состоит из нескольких компонентов, которые взаимодействуют друг с другом, а именно:

Ключевые компоненты

• Диспетчер процессов: многие базы данных имеют пул процессов/потоков, которые необходимо контролировать. Кроме того, в целях экономии наносекунд, некоторые современные базы данных используют собственные потоки вместо потоков операционной системы;
• Диспетчер сети: сетевой ввод-вывод - большая проблема, особенно для распределенных баз данных. Поэтому, у некоторых БД есть свой диспетчер сети;
• Менеджер файловой системы: чтение или запись на диск — ещё одно слабое место БД. Поэтому важно иметь менеджер, который будет идеально обрабатывать файловую систему операционки или полностью заменит её;
• Диспетчер памяти: чтобы избежать эпичных зависаний при чтении или записи на диск, требуется большое количество оперативной памяти. Но когда её много, вам неизбежно потребуется эффективный диспетчер памяти. Особенно когда много одновременных запросов, использующих память;
• Диспетчер безопасности учётных записей: для управления аутентификацией и авторизацией пользователей;
• Диспетчер клиентов: управляет клиентскими подключениями.

Утилиты

• Менеджер резервного копирования: для сохранения и восстановления базы данных;
• Диспетчер восстановления: обеспечивает целостность данных при перезапуске БД после падения;
• Диспетчер контроля: ведёт журнал активности базы данных и предоставляет инструменты для её мониторинга;
• Диспетчер администрирования: для хранения метаданных (например, названия и структуры таблиц), а также управления базами данных, схемами, табличными пространствами.

Диспетчер запросов

Парсер запросов: проверяет, является ли запрос допустимым;
Рерайтер: перезаписывает запрос;
Оптимизатор: оптимизирует запрос;
Исполнитель запросов: компилирует и выполняет запрос.

Диспетчер данных

Диспетчер транзакций: обрабатывает транзакции;
Диспетчер кэша: помещает данные в память перед их использованием и записью на диск;
Менеджер доступа к данным: предоставляет доступ к данным на диске.

Далее я подробно остановлюсь на том, как базы данных управляет SQL-запросами с помощью диспетчеров клиентов, запросов и данных (сюда же включу и диспетчера восстановления).

Диспетчер клиентов

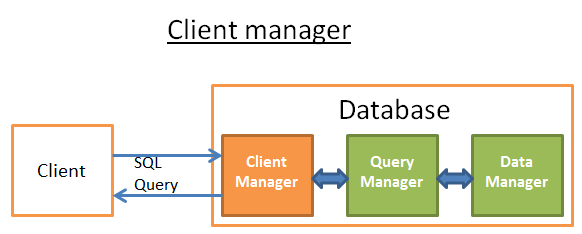
Диспетчер клиентов, как несложно догадаться, обрабатывает взиамодействия с клиентом. Клиентом может быть (веб) сервер или приложение конечного пользователя. Диспетчер клиентов предоставляет доступ к базе данных через различные API: JDBC, ODBC, OLE-DB, включая некоторые проприетарные API.

При подключении к БД диспетчер клиентов сначала проверяет аутентификацию (логин и пароль), затем - есть ли у вас полномочия на использование базы данных. Эти права доступа устанавливаются администратором БД. Затем диспетчер проверяет, не перегружена ли БД и есть ли свободный процесс (или поток) для обработки вашего запроса. Пока необходимая информация собирается, диспетчер ожидает. Если ожидание превышает тайм-аут, диспетчер разрывает соединение и возвращает сообщение об ошибке. В дальнейшем ваш запрос перенаправляется к диспетчеру запросов. После получения данных от диспетчера запросов, промежуточные результаты сохраняются в буфер и отправляются вам. В случае каких-то проблем, соединение разрывается, возвращается сообщение, объясняющее проблему, и процесс завершается.

Диспетчер запросов

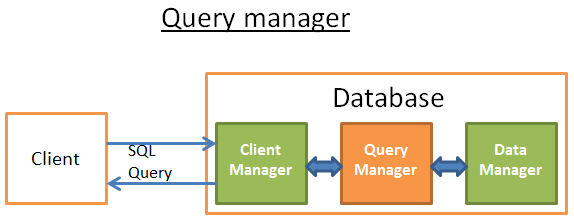
Вот здесь-то и раскрывается вся сила базы данных. В этой части БД плохо написанный запрос трансформируется в быстрый код, после выполнения которого результаты возвращаются диспетчеру клиентов. Этот процесс состоит из следующих шагов: сначала запрос анализируется на валидность; затем он перезаписывается — это предварительная оптимизация, удаляющая бесполезные операции; далее для улучшения производительности запрос оптимизируется в план исполнения и доступа к данным, который затем компилируется и выполняется.

Если вы хотите лучше понять все вышеописанные процессы, рекомендую почитать:

• Раннее исследование (1979) на тему оптимизации с учётом затрат: выбор пути доступа в реляционной системе управления базами данных. В статье всего 12 страниц, и она будет понятна человеку со средним уровнем компьютерной грамотности;
• А вот очень хорошая и подробная презентация о том, как DB2 9.Х оптимизирует запросы;
• Отличная презентация о том, как PostgreSQL оптимизирует запросы. Не сложная, потому что это презентация не про то, какие алгоритмы используются в PostgreSQL, а о планах запросов, которые создаёт PostgreSQL в разных ситуациях;
• Официальная документация SQLite об оптимизации запросов. Читать тоже не сложно, работают простые правила. Причем, это единственная официальная документация, которая на самом деле объясняет, как оно работает.
• Ещё одна годная презентация о том, как SQL Server 2005 оптимизирует запросы;
• Официальное описание оптимизации в Oracle 12с;
• 2 теоретических курса по оптимизации запросов от авторов книги “Системы управления БД” здесь и здесь. Интересные материалы про оптимизацию чтения и записи на диск, но не для новичков.
• Ещё один теоретический курс, он попроще, но акцент только на операции объединения и ввода-вывода.

Парсер запросов

Каждый SQL-оператор отправляется в парсер, где он проверяется на правильность синтаксиса. Если вы допустили ошибку, парсер отклонит запрос. Например, если вы написали “SLECT” вместо “SELECT”, на этом обработка вашего запроса закончится. Но это ещё не всё. Парсер также проверяет, что ключевые слова используются в правильном порядке. Например, если перед “SELECT” идёт “WHERE”, запрос будет отклонён. Затем анализируются таблицы и поля запроса. Парсер использует метаданные БД, чтобы проверить, существуют ли таблицы, поля в таблице, а также возможны ли операции для конкретных типов полей (например, нельзя сравнивать целое число со строкой, нельзя использовать substring() для целого числа). Затем проверяется, есть ли у вас разрешение на чтение (или редактирование) данных таблиц. Эти права доступа определяются администратором базы данных. Во время парсинга SQL-запрос преобразуется во внутреннее представление (часто дерево). Если все хорошо, внутреннее представление направляет запрос в рерайтер.

Рерайтер запросов

Итак, у нас есть внутреннее представление запроса. Основная цель рерайтера - предварительно оптимизировать запрос, чтобы избежать ненужных операций и помочь оптимизатору найти наилучшее решение. Рерайтер применяет определённый набор правил к запросу. Если запрос подходит под данное правило, правило применяется - запрос переписывается.

Вот неполный список правил:

• Слияние представлений: если вы используете представления, они преобразуются соответствующими алгоритмами SQL;
• Слияние подзапросов: подзапросы очень трудно оптимизировать, поэтому рерайтер попытается изменить запрос, чтобы избавиться от них.

Например:

1
2
3
4
5
6

SELECT PERSON.*
FROM PERSON
WHERE PERSON.person_key IN
(SELECT MAILS.person_key
FROM MAILS
WHERE MAILS.mail LIKE 'christophe%');

будет заменено на:

1
2
3
4

SELECT PERSON.*
FROM PERSON, MAILS
WHERE PERSON.person_key = MAILS.person_key
and MAILS.mail LIKE 'christophe%';

• Удаление лишних операторов: например, если вы используете DISTINCT, и одновременно UNIQUE, что не позволяет данным быть неуникальными, оператор DISTINCT удаляется;
• Удаление повторных объединений: если вы дважды использовали одно и то же условие объединения, например, одно из них скрыто в представлении, или если из-за транзитивности объединение повторяется, оно будет удалено;
• Постоянные арифметические вычисления: если ваш запрос требует вычислений, они будут произведены один раз в течение перезаписи. Например, WHERE AGE > 10+2 будет преобразовано в WHERE AGE > 12, а TODATE(“какая-нибудь дата”) преобразуется в дату в формате datetime;
• (дополнительно) Отсечение разделов: если вы используете секционированные таблицы, рерайтер может определить, какие разделы использовать;
• (дополнительно) Перезапись материализованных представлений: если у вас есть материализованное представление, которое соответствует подмножеству предикатов в запросе, рерайтер проверяет, актуально ли представление, и изменяет запрос, чтобы использовать материализованное представление вместо исходных таблиц;
• (дополнительно) Пользовательские правила: если у вас есть пользовательские правила для изменения запроса (например, политика Oracle), рерайтер выполняет эти правила;
• (дополнительно) OLAP преобразования: аналитические функции, звездообразные объединения, агрегирование также преобразуются (не уверен, делает ли это рерайтер или оптимизатор, скорее всего, зависит от конкретной БД).

Наконец, наш переписанный запрос передаётся оптимизатору запросов, где начинается самое интересное!

По мотивам Christophe

To be continued…

Читайте так же статьи по теме:

• Как работает реляционная база данных. Часть 2
• Как работает реляционная база данных. Часть 3